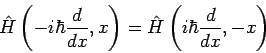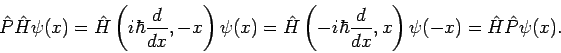Next: Dualer Raum. Ket- und
Up: Statistik der Messwerten im
Previous: Die Algebra der Kommutatoren
Contents
Wir interessieren uns für die zeitliche Änderung einer Messbaren 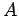 ,
,
Die Zeitliche Entwicklung der WF ist durch die SGl. gegeben:
und
Daher
Das mittlere Glied ist 0 wenn 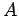 nicht explizit von der Zeit abhängig
ist. Unter Benutzung der SGl und der Hermite'schen Natur von
nicht explizit von der Zeit abhängig
ist. Unter Benutzung der SGl und der Hermite'schen Natur von 
Beispiel: Die Parität. Die Parität ist eine Observable
deren Operator (in 1d) durch
gegeben ist. 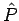 ist Hermite'sch, und
ist Hermite'sch, und 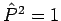 . Daher sind die EW von
. Daher sind die EW von 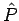
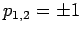 .
. 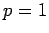 entspricht der geraden WF und
entspricht der geraden WF und 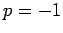 den ungeraden
WF. Wenn
den ungeraden
WF. Wenn 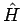 invariant gegen den Wechsel
invariant gegen den Wechsel
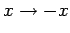 ist, so
kommutiert
ist, so
kommutiert 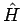 mit
mit 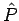 .
. 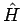 ist eine Fkt.
ist eine Fkt.
so gilt es für jede 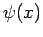
Wenn die WF bei 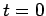 eine definierte Parität hat, so bleibt dieser Wert
erhalten. Die gleiche Eigenschaft gilt in höheren Dimensionen und
für die Vielteilchensysteme. Der Operator
eine definierte Parität hat, so bleibt dieser Wert
erhalten. Die gleiche Eigenschaft gilt in höheren Dimensionen und
für die Vielteilchensysteme. Der Operator 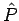 entspricht dann dem
Wechsel
entspricht dann dem
Wechsel
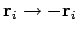 .
.




Next: Dualer Raum. Ket- und
Up: Statistik der Messwerten im
Previous: Die Algebra der Kommutatoren
Contents
Prof. Igor Sokolov
2005-02-14
![]() ,
,
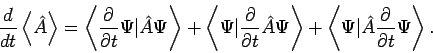
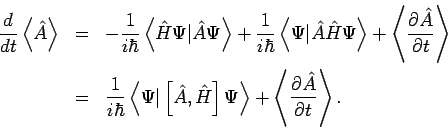
![$\left[ \hat{A},\hat{%
H}\right] =0$](img1525.png) gilt
gilt
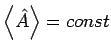 . Man sagt, dass
. Man sagt, dass ![$\left[ \hat{A},\hat{H}\right] =0$](img1528.png) so gilt auch
so gilt auch
![$\left[
e^{i\xi \hat{A}},\hat{H}\right] =0$](img1529.png) . Daher
. Daher
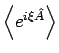 die charakteristische Fkt.
der Verteilung der Messergebnisse darstellt, bleibt diese Verteilung auch
zeitunabhängig.
die charakteristische Fkt.
der Verteilung der Messergebnisse darstellt, bleibt diese Verteilung auch
zeitunabhängig.