



Next: Bewegung in einem Coulomb-Feld.
Up: Quantenmechanik I WS 04/05
Previous: Schlussfolgerungen:
Contents
Wir betrachten die SGl mit einem Hamilton-Operator
mit
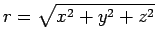 . Vergleichen wir den Laplace-Operator in
Kugelkoordinaten
. Vergleichen wir den Laplace-Operator in
Kugelkoordinaten
mit einem aus unserer vorherigen Vorlesung
so merken wir, dass
Der Hamilton-Operator ist eine Summe aus dem radialen Anteil, der
winkelunabhängig ist, und
![$1/\left[ 2J(r)\right] \mathbf{\hat{L}}^{2}$](img1135.png) mit
mit 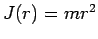 -Trägheitsmoment. Der Operator
-Trägheitsmoment. Der Operator
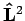 wirkt nur auf die Funktionen von
wirkt nur auf die Funktionen von 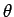 und
und 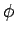 , und hängt nicht
von
, und hängt nicht
von 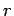 ab. Die SGl.
ab. Die SGl.
erlaubt dann die Variablentrennung: Wenn man annimmt, dass
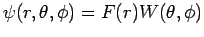 so erhält man
so erhält man
oder
Die Lösung bei beliebigen 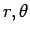 and
and 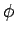 existiert nur dann,
wenn beide Teile der Gl. konstant sind. Diese Lösung muss der
natürlichen Randbedingungen genügen, d.h.
existiert nur dann,
wenn beide Teile der Gl. konstant sind. Diese Lösung muss der
natürlichen Randbedingungen genügen, d.h.
Die Lösungen für den Winkelanteil sind daher
die Abhängigkeit der WF von 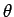 and
and 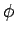 wird durch die Werte
wird durch die Werte
und
Der radiale Anteil der WF genügt dann der Gl.
Führen wir 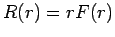 ein, so erhalten wir
ein, so erhalten wir
(die radiale SGl). Bei der qualitativen Untersuchung der Bewegung enspricht
der Term
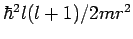 der ''effektiven potentiellen Energie''.
der ''effektiven potentiellen Energie''.
Subsections




Next: Bewegung in einem Coulomb-Feld.
Up: Quantenmechanik I WS 04/05
Previous: Schlussfolgerungen:
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{displaymath}
\hat{H}=\frac{-\hbar ^{2}}{2m}\left[ \frac{1}{r^{2}}\frac{\p...
...\frac{\partial ^{2}}{\partial
\phi ^{2}}\right) \right] +U(r)
\end{displaymath}](img1132.png)
![\begin{displaymath}
\mathbf{\hat{L}}^{2}=-\hbar ^{2}\left[ \frac{1}{\sin \theta ...
...2}\theta }\frac{\partial ^{2}}{\partial \phi ^{2}}%
\right] ,
\end{displaymath}](img1133.png)
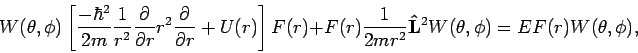
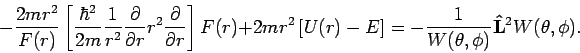
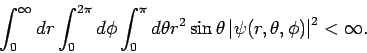
![\begin{displaymath}
-\frac{2mr^{2}}{F(r)}\left[ \frac{\hbar ^{2}}{2m}\frac{1}{r^...
...\right]
F(r)+2mr^{2}\left[ U(r)-E\right] -\hbar ^{2}l(l+1)=0.
\end{displaymath}](img1145.png)
![\begin{displaymath}
-\frac{\hbar ^{2}}{2m}\frac{d^{2}}{dr^{2}}R+\left[ U(r)+\frac{\hbar
^{2}l(l+1)}{2mr^{2}}\right] =ER
\end{displaymath}](img1147.png)